Researcher
Phone:
+49 711 685 88123
Open Master Thesis - Contact a supervisor for more details!
Over the past few years, knowledge graphs have emerged to address the need of extracting and combining multiple data sources [5]. Their flexible structure makes them suitable to integrate heterogeneous data. This has propelled many advances in query processing over knowledge graphs. However, the aspect of providing provenance explanations for query answers has not been satisfactorily solved. There are different types of provenance annotations [1, 4]. In this research project, we focus on how-provenance because it abstracts multiple types of annotations. How-provenance consists of annotating answers with polynomials with natural coefficients, whose variables are interpreted as the sources that witness the answer [2].
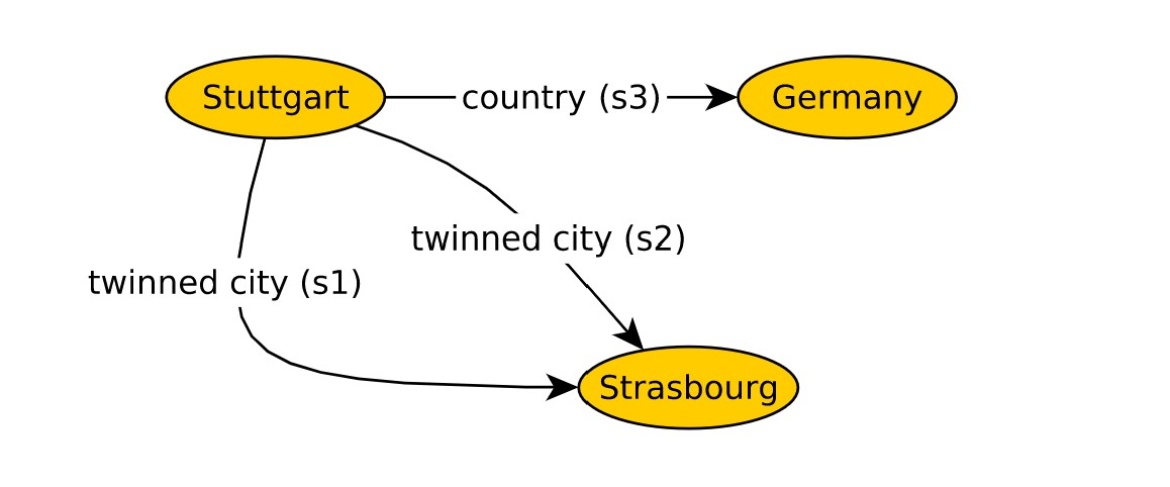
To illustrate the idea of polynomials, consider the following table containing the assertions and provenance of a knowledge graph.
| Assertion | Provenance |
| Stuttgart has twinned city Strasbourg | s1 = Stuttgart Administration |
| Stuttgart has twinned city Strasbourg | s2 = Stuttgart Tourism Website |
| Stuttgart is in country Germany | s3 = German Wikipedia |
The assertions and the provenance presented in the table above are depicted as
a knowledge graph in the following figure.
Each edge corresponds to an assertion in the table, and the provenance of the assertions is stated in parentheses.
Strasbourg is an answer to the query asking for twinned cities of cities in Germany. This answer is annotated with a polynomial (s1⊕s2)⊗s3. The polynomial does not only tell us the involved sources, but also how they are combined. Intuitively, to obtain the answer, we can use either source s1 or source s2, and then combine the chosen source with source s3.
Strasbourg is an answer to the query asking for twinned cities of cities in Germany. This answer is annotated with a polynomial (s1⊕s2)⊗s3. The polynomial does not only tell us the involved sources, but also how they are combined. Intuitively, to obtain the answer, we can use either source s1 or source s2, and then combine the chosen source with source s3.
The World Wide Web Consortium proposes SPARQL as the standard to query knowledge graphs on the Web. A recent paper [3] proposes a way to compute how-provenance for SPARQL queries via query rewriting. That is, to compute the provenance of the answers of a SPARQL query Q1, query Q1 is translated into a SPARQL query Q2 whose answers contain additional information codifying the provenance polynomial of each answer of query Q1.
The goal of the research project described herein is to define a method to produce succinct annotations for answers of SPARQL queries via query rewriting. In [3], the authors describe a method as desired, except that that does not produce succinct annotations. For instance, instead of annotating the aforementioned answer Strasbourg with the polynomial expression (s1 ⊕ s2) ⊗ s3, the method annotates it with the polynomial expression (s1 ⊗ s3) ⊕ (s2 ⊗ s3). Producing succinct annotations can benefit the generation, storage and use of polynomials. This is specially relevant for answers that can be produced in many alternative ways.
The goal of the research project described herein is to define a method to produce succinct annotations for answers of SPARQL queries via query rewriting. In [3], the authors describe a method as desired, except that that does not produce succinct annotations. For instance, instead of annotating the aforementioned answer Strasbourg with the polynomial expression (s1 ⊕ s2) ⊗ s3, the method annotates it with the polynomial expression (s1 ⊗ s3) ⊕ (s2 ⊗ s3). Producing succinct annotations can benefit the generation, storage and use of polynomials. This is specially relevant for answers that can be produced in many alternative ways.
The overall idea of this project is that to compute the how-provenance efficiently we can rewrite the original query Q1 in several queries {Q2, . . . , Qn}, instead of one, as proposed in [3]. This problem is not simple because separating a query can produce more intermediate results. The major research question that will be addressed in this project is how to rewrite the query to compute how-provenance efficiently.
Requirements
- Familiarity with database foundations (e.g., relational algebra).
- Experience with Semantic Web technologies (RDF and SPARQL).
References
- [1] James Cheney, Laura Chiticariu, and Wang Chiew Tan. “Provenance in Databases: Why, How, and Where”. In: Found. Trends Databases 1.4 (2009), pp. 379–474.
- [2] Todd J. Green, Gregory Karvounarakis, and Val Tannen. “Provenance semirings”. In: PODS. ACM, 2007, pp. 31–40.
- [3] Daniel Hernández, Luis Galárraga, and Katja Hose. “Computing How-Provenance for SPARQL Queries via Query Rewriting”. In: Proc. VLDB Endow. 14.13 (2021), pp. 3389–3401.
- [4] Melanie Herschel, Ralf Diestelkämper, and Houssem Ben Lahmar. “A survey on provenance: What for? What form? What from?” In: VLDB J. 26.6 (2017), pp. 881–906.
- [5] Aidan Hogan et al. Knowledge Graphs. Synthesis Lectures on Data, Semantics, and Knowledge. Morgan & Claypool Publishers, 2021.
Supervisors
Researcher
Phone:
+49 711 685 88109
Researcher
Phone:
+49 711 685 88133
Researcher
Phone:
+49 711 685 88116